Types of fluid flow

Types of fluid flow
What is fluid flow?
Flow of fluid deals with fluid dynamics and is a part of fluid mechanics which involves motion of the fluid flowing and the unbalanced forces subjected to them. The fluid will flow until the unbalanced forces applied to them are balanced.
Classification of fluid flow:
Flow of fluid can be classified as:
Ideal fluid flow:
Ideal fluid are those fluid in which density is constant which means it is incompressible and are inviscid (dynamic viscosity is zero). Therefore the ideal fluid flow is that type of flow in which the flow is incompressible as well as inviscid.
From Newton’s law of viscosity,
τ = µ du/dy
Therefore, τ = 0 (because dynamic viscosity, µ is zero).
Ideal fluid is hypothetical fluid which does not exist in nature but we study about ideal fluid because real fluid behavior is very similar to ideal fluid above the boundary layer (boundary layer is that region in which there is relative velocity between fluids layer).
For ideal fluid flow
- There will be no shear stress.
- Only normal stress acting on the fluid (normal stress acting on fluid at a point is equal to the pressure at that point).
- Force acting on the body or solid body due to the fluid, this force will be normal to the solid surface.
Steady flow and Unsteady flow:
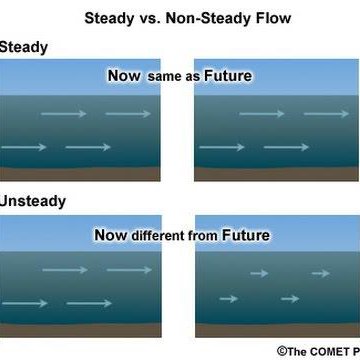
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are not changing or invariant with respect to time such a flow is called steady flow.
Therefore, mathematically, for steady flow
(∂V/ ∂t) x˳, y˳, z˳ = 0,
(∂p/ ∂t) x˳, y˳, z˳ = 0,
(∂ρ/ ∂t) x˳, y˳, z˳ = 0.
Where, x˳, y˳, z˳ represents fixed point in a fluid flow.
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are changing or variant with respect to time such a flow is called unsteady flow.
Therefore, mathematically, for unsteady flow
(∂V/ ∂t) x˳, y˳, z˳is not equal to zero,
(∂p/ ∂t) x˳, y˳, z˳ is not equal to zero,
(∂ρ/ ∂t) x˳, y˳, z˳ is not equal to zero.
Where, x˳, y˳, z˳ represents fixed point in a fluid flow.
Uniform flow and Non – uniform flow:
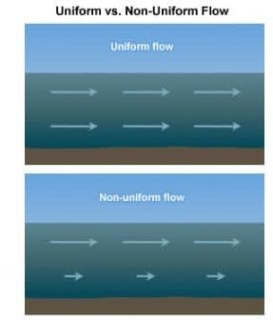
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are not changing or invariant with respect to space (or directions) for a constant time such a flow is called uniform flow.
Therefore, mathematically, for uniform flow
(∂V/ ∂s) t = constant = 0,
(∂p/ ∂s) t = constant = 0,
(∂ρ/ ∂s) t = constant = 0.
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are changing or variant with respect to space (or directions)for a constant time such a flow is called non – uniform flow.
Therefore, mathematically, for non – uniform flow
(∂V/ ∂s) t = constant is not equal to zero,
(∂p/ ∂s) t = constant is not equal to zero,
(∂ρ/ ∂s) t = constant is not equal to zero.
Steady and uniform flow:
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are not changing or invariant with respect to space (or directions) and time such a flow is called steady uniform flow.
Therefore, mathematically
(∂V/ ∂t) x˳, y˳, z˳, (∂V/ ∂s) t = constant = 0,
(∂p/ ∂t) x˳, y˳, z˳, (∂p/ ∂s) t = constant = 0,
(∂ρ/ ∂t) x˳, y˳, z˳, (∂ρ/ ∂s) t = constant = 0.
Non – uniform and unsteady flow:
In any fluid flow the fluid properties like density, pressure and velocity of fluid particles are changing or variant with respect to space (or directions) and time such a flow is called steady uniform flow.
Therefore, mathematically
(∂V/ ∂t) x˳, y˳, z˳, (∂V/ ∂s) t = constantis not equal to zero,
(∂p/ ∂t) x˳, y˳, z˳, (∂p/ ∂s) t = constantis not equal to zero,
(∂ρ/ ∂t) x˳, y˳, z˳, (∂ρ/ ∂s) t = constantis not equal to zero.
Laminar flow and Turbulent flow:
Laminar flow are the flow in which the fluid particle move in a stream line or well defined paths and all the stream lines are parallel and straight. Therefore the fluid particles move in layers or laminas which gliding smoothly over the adjacent layer.
Turbulent flow are the flow in which fluid particles moves in zigzag way. Eddies formation takes place due to the movement of fluid particle in zigzag way which results in high energy loss.
Reynolds number is used to determine the type of flow in pipe flow by,
Re = VD/ ʋ
Where, Re = Reynolds number
V = Mean velocity of flow in pipe,
ʋ = Kinematic viscosity of fluid.
Reynolds number is a non – dimensional number.
When the value of Reynolds number is less than 2000 then the fluid flow is known as laminar flow, when the value of Reynolds number is more than 4000 then the fluid flow is known as turbulent flow, When the value of Reynolds number is in between 2000 and 4000 then the fluid flow is known as transition flow.
Compressible flow and Incompressible flow:
Compressible flow are that type of flow in which density of the fluid changes or variant from one point to another point or are not constant with respect to pressure for the fluid.
(∂ρ/ ∂p) is not equal to zero.
Incompressible flow are that type of flow in which density of the fluid does not changes or invariant from one point to another point or are constant with respect to pressure for the fluid.
(∂ρ/ ∂p) is equal to zero.
Rotational flow and Irrotational flow:
Rotational flow are defined as that type of flow in which fluid particles moves in stream lines as well as rotate about their axis.
Irrotational flow is defined as that type of flow in which fluid particle moving along stream line does not rotate about their axis.
One – dimensional flow, two – dimensional flow, three – dimensional flow:
When flow of fluid takes place in only one direction which means the flow variables like displacement, velocity and acceleration are changing in only one direction then the flow is called one – dimensional flow.
u = f (x), v = 0 and w = 0.
When flow of fluid takes place in two direction which means the flow variables like displacement, velocity and acceleration are changing in two direction then the flow is called two – dimensional flow.
u = f 1 (x, y), v = f 2 (x, y) and w = 0.
When flow of fluid takes place in three direction which means the flow variables like displacement, velocity and acceleration are changing in all three direction then the flow is called three – dimensional flow.
u = f1 (x, y, z), v = f2 (x, y, z) and w = f 3 (x, y, z).
Vortex flow
Vortex flow are that type of flow in which fluid flow along curved path. It is of two types
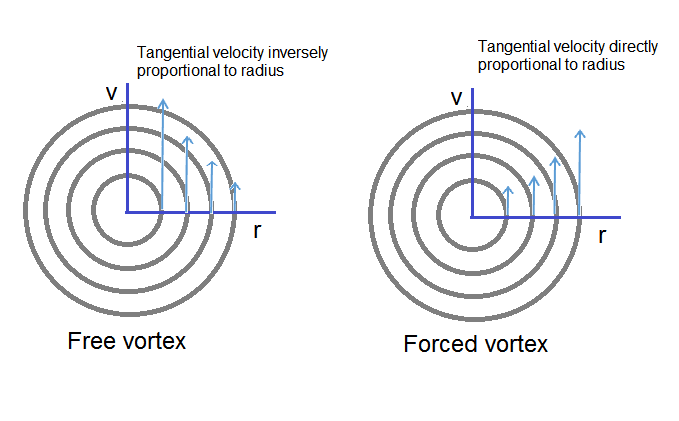
- Forced vortex flow: It is defined as that type of flow in which external torque is needed for rotating the fluid mass and the fluid mass in this type of flow rotates with constant angular velocity ω and the tangential velocity of the particles of fluid is v = ω x r
Where r is equal to the radius of fluid particle which is from the axis of rotation.
Example: Fluid flow inside the impeller of centrifugal pump, fluid flow through the runner of turbine.
- Free vortex flow: It is defined as that type of flow in which no external torque is needed for rotating the fluid mass. Therefore in free vortex flow, fluid rotate due to the rotation previously imparted to the fluid.
Example: Whirlpool in river, fluid flow in circular bend of pipe, fluid flowing in centrifugal pump casing.